Trends and cycles in unemployment¶
Here we consider three methods for separating a trend and cycle in economic data. Supposing we have a time series \(y_t\), the basic idea is to decompose it into these two components:
where \(\mu_t\) represents the trend or level and \(\eta_t\) represents the cyclical component. In this case, we consider a stochastic trend, so that \(\mu_t\) is a random variable and not a deterministic function of time. Two of methods fall under the heading of “unobserved components” models, and the third is the popular Hodrick-Prescott (HP) filter. Consistent with e.g. Harvey and Jaeger (1993), we find that these models all produce similar decompositions.
This notebook demonstrates applying these models to separate trend from cycle in the U.S. unemployment rate.
[1]:
%matplotlib inline
[2]:
import numpy as np
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
[3]:
from pandas_datareader.data import DataReader
endog = DataReader('UNRATE', 'fred', start='1954-01-01')
endog.index.freq = endog.index.inferred_freq
Hodrick-Prescott (HP) filter¶
The first method is the Hodrick-Prescott filter, which can be applied to a data series in a very straightforward method. Here we specify the parameter \(\lambda=129600\) because the unemployment rate is observed monthly.
[4]:
hp_cycle, hp_trend = sm.tsa.filters.hpfilter(endog, lamb=129600)
Unobserved components and ARIMA model (UC-ARIMA)¶
The next method is an unobserved components model, where the trend is modeled as a random walk and the cycle is modeled with an ARIMA model - in particular, here we use an AR(4) model. The process for the time series can be written as:
where \(\phi(L)\) is the AR(4) lag polynomial and \(\epsilon_t\) and \(\nu_t\) are white noise.
[5]:
mod_ucarima = sm.tsa.UnobservedComponents(endog, 'rwalk', autoregressive=4)
# Here the powell method is used, since it achieves a
# higher loglikelihood than the default L-BFGS method
res_ucarima = mod_ucarima.fit(method='powell', disp=False)
print(res_ucarima.summary())
Unobserved Components Results
==============================================================================
Dep. Variable: UNRATE No. Observations: 851
Model: random walk Log Likelihood -463.920
+ AR(4) AIC 939.840
Date: Mon, 16 Dec 2024 BIC 968.311
Time: 11:22:46 HQIC 950.746
Sample: 01-01-1954
- 11-01-2024
Covariance Type: opg
================================================================================
coef std err z P>|z| [0.025 0.975]
--------------------------------------------------------------------------------
sigma2.level 6.188e-08 0.011 5.51e-06 1.000 -0.022 0.022
sigma2.ar 0.1739 0.015 11.612 0.000 0.145 0.203
ar.L1 1.0258 0.019 54.276 0.000 0.989 1.063
ar.L2 -0.1061 0.016 -6.619 0.000 -0.137 -0.075
ar.L3 0.0752 0.023 3.250 0.001 0.030 0.121
ar.L4 -0.0261 0.019 -1.387 0.165 -0.063 0.011
===================================================================================
Ljung-Box (L1) (Q): 0.00 Jarque-Bera (JB): 6726559.75
Prob(Q): 0.97 Prob(JB): 0.00
Heteroskedasticity (H): 9.11 Skew: 17.48
Prob(H) (two-sided): 0.00 Kurtosis: 437.40
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
Unobserved components with stochastic cycle (UC)¶
The final method is also an unobserved components model, but where the cycle is modeled explicitly.
[6]:
mod_uc = sm.tsa.UnobservedComponents(
endog, 'rwalk',
cycle=True, stochastic_cycle=True, damped_cycle=True,
)
# Here the powell method gets close to the optimum
res_uc = mod_uc.fit(method='powell', disp=False)
# but to get to the highest loglikelihood we do a
# second round using the L-BFGS method.
res_uc = mod_uc.fit(res_uc.params, disp=False)
print(res_uc.summary())
Unobserved Components Results
=====================================================================================
Dep. Variable: UNRATE No. Observations: 851
Model: random walk Log Likelihood -472.703
+ damped stochastic cycle AIC 953.407
Date: Mon, 16 Dec 2024 BIC 972.378
Time: 11:22:48 HQIC 960.675
Sample: 01-01-1954
- 11-01-2024
Covariance Type: opg
===================================================================================
coef std err z P>|z| [0.025 0.975]
-----------------------------------------------------------------------------------
sigma2.level 0.0187 0.034 0.557 0.578 -0.047 0.085
sigma2.cycle 0.1529 0.033 4.650 0.000 0.088 0.217
frequency.cycle 0.0436 0.029 1.488 0.137 -0.014 0.101
damping.cycle 0.9560 0.019 50.938 0.000 0.919 0.993
===================================================================================
Ljung-Box (L1) (Q): 1.55 Jarque-Bera (JB): 6630408.35
Prob(Q): 0.21 Prob(JB): 0.00
Heteroskedasticity (H): 9.47 Skew: 17.35
Prob(H) (two-sided): 0.00 Kurtosis: 434.80
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
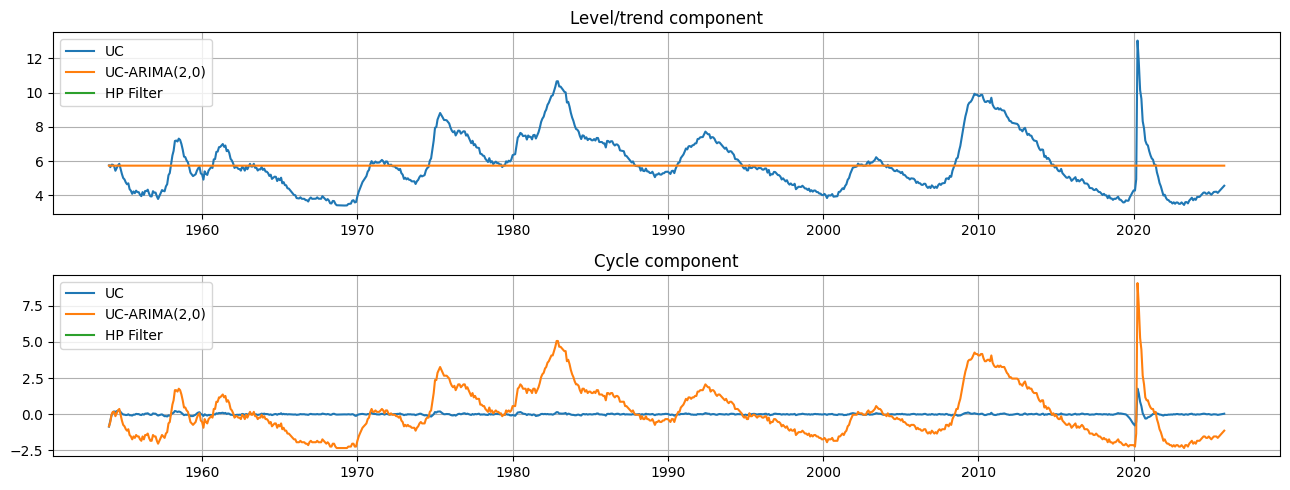
Graphical comparison¶
The output of each of these models is an estimate of the trend component \(\mu_t\) and an estimate of the cyclical component \(\eta_t\). Qualitatively the estimates of trend and cycle are very similar, although the trend component from the HP filter is somewhat more variable than those from the unobserved components models. This means that relatively mode of the movement in the unemployment rate is attributed to changes in the underlying trend rather than to temporary cyclical movements.
[7]:
fig, axes = plt.subplots(2, figsize=(13,5));
axes[0].set(title='Level/trend component')
axes[0].plot(endog.index, res_uc.level.smoothed, label='UC')
axes[0].plot(endog.index, res_ucarima.level.smoothed, label='UC-ARIMA(2,0)')
axes[0].plot(hp_trend, label='HP Filter')
axes[0].legend(loc='upper left')
axes[0].grid()
axes[1].set(title='Cycle component')
axes[1].plot(endog.index, res_uc.cycle.smoothed, label='UC')
axes[1].plot(endog.index, res_ucarima.autoregressive.smoothed, label='UC-ARIMA(2,0)')
axes[1].plot(hp_cycle, label='HP Filter')
axes[1].legend(loc='upper left')
axes[1].grid()
fig.tight_layout();
