Prediction (out of sample)¶
[1]:
%matplotlib inline
[2]:
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
plt.rc("figure", figsize=(16, 8))
plt.rc("font", size=14)
Artificial data¶
[3]:
nsample = 50
sig = 0.25
x1 = np.linspace(0, 20, nsample)
X = np.column_stack((x1, np.sin(x1), (x1 - 5) ** 2))
X = sm.add_constant(X)
beta = [5.0, 0.5, 0.5, -0.02]
y_true = np.dot(X, beta)
y = y_true + sig * np.random.normal(size=nsample)
Estimation¶
[4]:
olsmod = sm.OLS(y, X)
olsres = olsmod.fit()
print(olsres.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.986
Model: OLS Adj. R-squared: 0.985
Method: Least Squares F-statistic: 1064.
Date: Wed, 02 Nov 2022 Prob (F-statistic): 1.74e-42
Time: 17:06:17 Log-Likelihood: 4.4594
No. Observations: 50 AIC: -0.9188
Df Residuals: 46 BIC: 6.729
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 4.9488 0.079 62.924 0.000 4.791 5.107
x1 0.5124 0.012 42.246 0.000 0.488 0.537
x2 0.6093 0.048 12.778 0.000 0.513 0.705
x3 -0.0216 0.001 -20.250 0.000 -0.024 -0.019
==============================================================================
Omnibus: 6.272 Durbin-Watson: 2.752
Prob(Omnibus): 0.043 Jarque-Bera (JB): 5.171
Skew: 0.723 Prob(JB): 0.0754
Kurtosis: 3.625 Cond. No. 221.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
In-sample prediction¶
[5]:
ypred = olsres.predict(X)
print(ypred)
[ 4.40969647 4.94512482 5.43363276 5.84201378 6.14904543 6.34897612
6.45247004 6.48485512 6.48196167 6.48423561 6.53009328 6.64960978
6.85957769 7.16074809 7.53770719 7.96140876 8.39394633 8.79478112
9.12740246 9.36532639 9.49644688 9.52502482 9.470988 9.36665699
9.25143498 9.16533394 9.14240078 9.20512354 9.36073664 9.60003232
9.89887343 10.22215909 10.52959169 10.78229764 10.94921423 11.01219312
10.96898204 10.83359489 10.63400924 10.40756972 10.19485242 10.03299831
9.94961111 9.95822208 10.05606687 10.22453968 10.43225015 10.64018073
10.80809711 10.90115863]
Create a new sample of explanatory variables Xnew, predict and plot¶
[6]:
x1n = np.linspace(20.5, 25, 10)
Xnew = np.column_stack((x1n, np.sin(x1n), (x1n - 5) ** 2))
Xnew = sm.add_constant(Xnew)
ynewpred = olsres.predict(Xnew) # predict out of sample
print(ynewpred)
[10.87960032 10.69855331 10.38191219 9.98412967 9.57688468 9.23153285
9.00163619 8.90984922 8.94237236 9.05233055]
Plot comparison¶
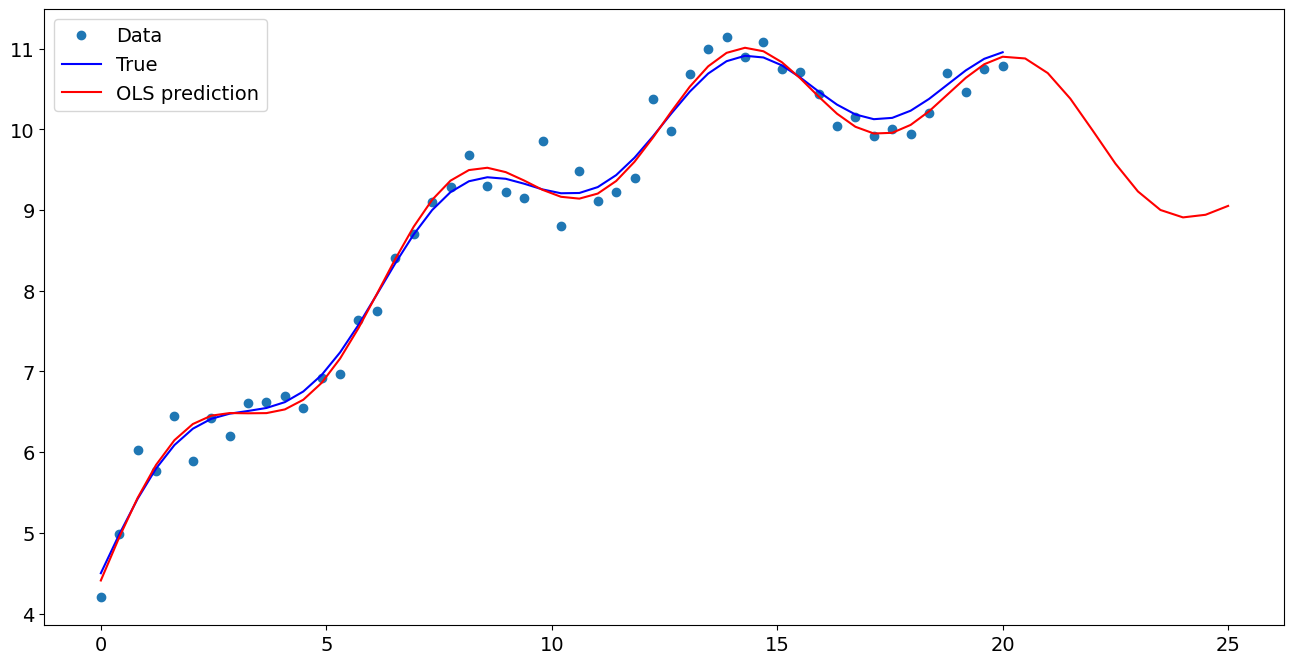
[7]:
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
ax.plot(x1, y, "o", label="Data")
ax.plot(x1, y_true, "b-", label="True")
ax.plot(np.hstack((x1, x1n)), np.hstack((ypred, ynewpred)), "r", label="OLS prediction")
ax.legend(loc="best")
[7]:
<matplotlib.legend.Legend at 0x7fc0436f7010>
Predicting with Formulas¶
Using formulas can make both estimation and prediction a lot easier
[8]:
from statsmodels.formula.api import ols
data = {"x1": x1, "y": y}
res = ols("y ~ x1 + np.sin(x1) + I((x1-5)**2)", data=data).fit()
We use the I to indicate use of the Identity transform. Ie., we do not want any expansion magic from using **2
[9]:
res.params
[9]:
Intercept 4.948842
x1 0.512418
np.sin(x1) 0.609303
I((x1 - 5) ** 2) -0.021566
dtype: float64
Now we only have to pass the single variable and we get the transformed right-hand side variables automatically
[10]:
res.predict(exog=dict(x1=x1n))
[10]:
0 10.879600
1 10.698553
2 10.381912
3 9.984130
4 9.576885
5 9.231533
6 9.001636
7 8.909849
8 8.942372
9 9.052331
dtype: float64