Robust Linear Models¶
[1]:
%matplotlib inline
[2]:
import matplotlib.pyplot as plt
import numpy as np
import statsmodels.api as sm
Estimation¶
Load data:
[3]:
data = sm.datasets.stackloss.load()
data.exog = sm.add_constant(data.exog)
Huber’s T norm with the (default) median absolute deviation scaling
[4]:
huber_t = sm.RLM(data.endog, data.exog, M=sm.robust.norms.HuberT())
hub_results = huber_t.fit()
print(hub_results.params)
print(hub_results.bse)
print(
hub_results.summary(
yname="y", xname=["var_%d" % i for i in range(len(hub_results.params))]
)
)
const -41.026498
AIRFLOW 0.829384
WATERTEMP 0.926066
ACIDCONC -0.127847
dtype: float64
const 9.791899
AIRFLOW 0.111005
WATERTEMP 0.302930
ACIDCONC 0.128650
dtype: float64
Robust linear Model Regression Results
==============================================================================
Dep. Variable: y No. Observations: 21
Model: RLM Df Residuals: 17
Method: IRLS Df Model: 3
Norm: HuberT
Scale Est.: mad
Cov Type: H1
Date: Wed, 02 Nov 2022
Time: 17:06:58
No. Iterations: 19
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
var_0 -41.0265 9.792 -4.190 0.000 -60.218 -21.835
var_1 0.8294 0.111 7.472 0.000 0.612 1.047
var_2 0.9261 0.303 3.057 0.002 0.332 1.520
var_3 -0.1278 0.129 -0.994 0.320 -0.380 0.124
==============================================================================
If the model instance has been used for another fit with different fit parameters, then the fit options might not be the correct ones anymore .
Huber’s T norm with ‘H2’ covariance matrix
[5]:
hub_results2 = huber_t.fit(cov="H2")
print(hub_results2.params)
print(hub_results2.bse)
const -41.026498
AIRFLOW 0.829384
WATERTEMP 0.926066
ACIDCONC -0.127847
dtype: float64
const 9.089504
AIRFLOW 0.119460
WATERTEMP 0.322355
ACIDCONC 0.117963
dtype: float64
Andrew’s Wave norm with Huber’s Proposal 2 scaling and ‘H3’ covariance matrix
[6]:
andrew_mod = sm.RLM(data.endog, data.exog, M=sm.robust.norms.AndrewWave())
andrew_results = andrew_mod.fit(scale_est=sm.robust.scale.HuberScale(), cov="H3")
print("Parameters: ", andrew_results.params)
Parameters: const -40.881796
AIRFLOW 0.792761
WATERTEMP 1.048576
ACIDCONC -0.133609
dtype: float64
See help(sm.RLM.fit) for more options and module sm.robust.scale for scale options
Comparing OLS and RLM¶
Artificial data with outliers:
[7]:
nsample = 50
x1 = np.linspace(0, 20, nsample)
X = np.column_stack((x1, (x1 - 5) ** 2))
X = sm.add_constant(X)
sig = 0.3 # smaller error variance makes OLS<->RLM contrast bigger
beta = [5, 0.5, -0.0]
y_true2 = np.dot(X, beta)
y2 = y_true2 + sig * 1.0 * np.random.normal(size=nsample)
y2[[39, 41, 43, 45, 48]] -= 5 # add some outliers (10% of nsample)
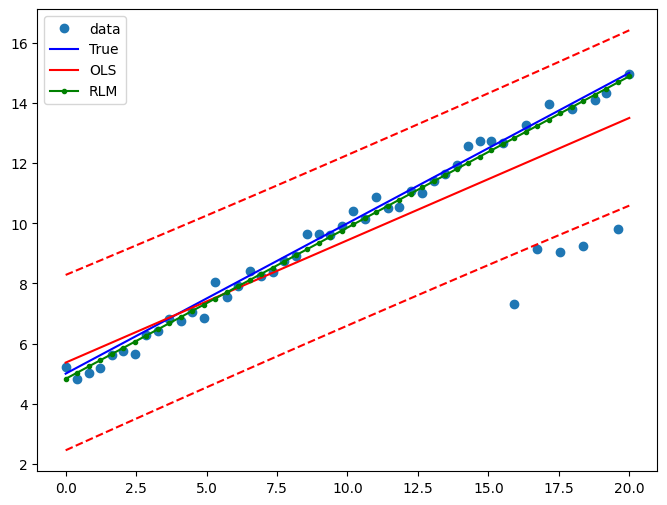
Example 1: quadratic function with linear truth¶
Note that the quadratic term in OLS regression will capture outlier effects.
[8]:
res = sm.OLS(y2, X).fit()
print(res.params)
print(res.bse)
print(res.predict())
[ 4.78516573 0.55123012 -0.01444285]
[0.44525161 0.06874084 0.0060825 ]
[ 4.42409451 4.70563066 4.98235453 5.25426612 5.52136544 5.78365248
6.04112723 6.29378972 6.54163992 6.78467784 7.02290349 7.25631686
7.48491795 7.70870677 7.92768331 8.14184756 8.35119955 8.55573925
8.75546667 8.95038182 9.14048469 9.32577528 9.5062536 9.68191964
9.85277339 10.01881488 10.18004408 10.336461 10.48806565 10.63485802
10.77683811 10.91400593 11.04636146 11.17390472 11.2966357 11.41455441
11.52766083 11.63595498 11.73943685 11.83810644 11.93196376 12.02100879
12.10524155 12.18466203 12.25927024 12.32906616 12.39404981 12.45422118
12.50958027 12.56012709]
Estimate RLM:
[9]:
resrlm = sm.RLM(y2, X).fit()
print(resrlm.params)
print(resrlm.bse)
[ 4.68933411e+00 5.38229820e-01 -3.74367086e-03]
[0.11236366 0.01734743 0.00153498]
Draw a plot to compare OLS estimates to the robust estimates:
[10]:
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111)
ax.plot(x1, y2, "o", label="data")
ax.plot(x1, y_true2, "b-", label="True")
pred_ols = res.get_prediction()
iv_l = pred_ols.summary_frame()["obs_ci_lower"]
iv_u = pred_ols.summary_frame()["obs_ci_upper"]
ax.plot(x1, res.fittedvalues, "r-", label="OLS")
ax.plot(x1, iv_u, "r--")
ax.plot(x1, iv_l, "r--")
ax.plot(x1, resrlm.fittedvalues, "g.-", label="RLM")
ax.legend(loc="best")
[10]:
<matplotlib.legend.Legend at 0x7f88c4387b20>
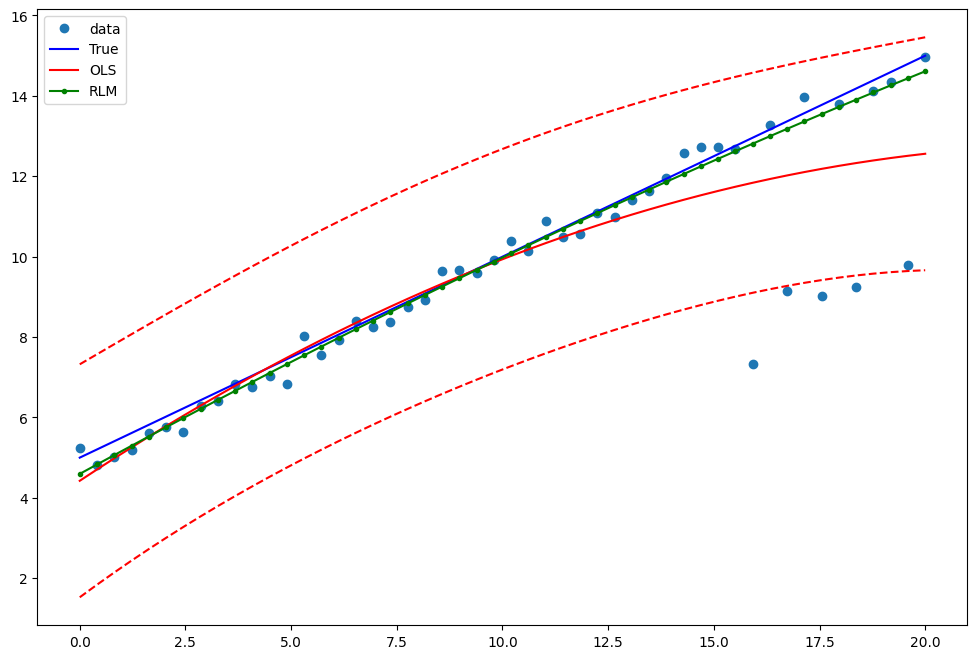
Example 2: linear function with linear truth¶
Fit a new OLS model using only the linear term and the constant:
[11]:
X2 = X[:, [0, 1]]
res2 = sm.OLS(y2, X2).fit()
print(res2.params)
print(res2.bse)
[5.36730096 0.40680163]
[0.38922146 0.03353689]
Estimate RLM:
[12]:
resrlm2 = sm.RLM(y2, X2).fit()
print(resrlm2.params)
print(resrlm2.bse)
[4.82751717 0.50304602]
[0.09082931 0.00782622]
Draw a plot to compare OLS estimates to the robust estimates:
[13]:
pred_ols = res2.get_prediction()
iv_l = pred_ols.summary_frame()["obs_ci_lower"]
iv_u = pred_ols.summary_frame()["obs_ci_upper"]
fig, ax = plt.subplots(figsize=(8, 6))
ax.plot(x1, y2, "o", label="data")
ax.plot(x1, y_true2, "b-", label="True")
ax.plot(x1, res2.fittedvalues, "r-", label="OLS")
ax.plot(x1, iv_u, "r--")
ax.plot(x1, iv_l, "r--")
ax.plot(x1, resrlm2.fittedvalues, "g.-", label="RLM")
legend = ax.legend(loc="best")