Quasi-binomial regression¶
This notebook demonstrates using custom variance functions and non-binary data with the quasi-binomial GLM family to perform a regression analysis using a dependent variable that is a proportion.
The notebook uses the barley leaf blotch data that has been discussed in several textbooks. See below for one reference:
[1]:
import statsmodels.api as sm
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from io import StringIO
The raw data, expressed as percentages. We will divide by 100 to obtain proportions.
[2]:
raw = StringIO("""0.05,0.00,1.25,2.50,5.50,1.00,5.00,5.00,17.50
0.00,0.05,1.25,0.50,1.00,5.00,0.10,10.00,25.00
0.00,0.05,2.50,0.01,6.00,5.00,5.00,5.00,42.50
0.10,0.30,16.60,3.00,1.10,5.00,5.00,5.00,50.00
0.25,0.75,2.50,2.50,2.50,5.00,50.00,25.00,37.50
0.05,0.30,2.50,0.01,8.00,5.00,10.00,75.00,95.00
0.50,3.00,0.00,25.00,16.50,10.00,50.00,50.00,62.50
1.30,7.50,20.00,55.00,29.50,5.00,25.00,75.00,95.00
1.50,1.00,37.50,5.00,20.00,50.00,50.00,75.00,95.00
1.50,12.70,26.25,40.00,43.50,75.00,75.00,75.00,95.00""")
The regression model is a two-way additive model with site and variety effects. The data are a full unreplicated design with 10 rows (sites) and 9 columns (varieties).
[3]:
df = pd.read_csv(raw, header=None)
df = df.melt()
df["site"] = 1 + np.floor(df.index / 10).astype(np.int)
df["variety"] = 1 + (df.index % 10)
df = df.rename(columns={"value": "blotch"})
df = df.drop("variable", axis=1)
df["blotch"] /= 100
Fit the quasi-binomial regression with the standard variance function.
[4]:
model1 = sm.GLM.from_formula("blotch ~ 0 + C(variety) + C(site)",
family=sm.families.Binomial(), data=df)
result1 = model1.fit(scale="X2")
print(result1.summary())
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: blotch No. Observations: 90
Model: GLM Df Residuals: 72
Model Family: Binomial Df Model: 17
Link Function: logit Scale: 0.088778
Method: IRLS Log-Likelihood: -20.791
Date: Tue, 02 Feb 2021 Deviance: 6.1260
Time: 06:54:50 Pearson chi2: 6.39
No. Iterations: 10
Covariance Type: nonrobust
==================================================================================
coef std err z P>|z| [0.025 0.975]
----------------------------------------------------------------------------------
C(variety)[1] -8.0546 1.422 -5.664 0.000 -10.842 -5.268
C(variety)[2] -7.9046 1.412 -5.599 0.000 -10.672 -5.138
C(variety)[3] -7.3652 1.384 -5.321 0.000 -10.078 -4.652
C(variety)[4] -7.0065 1.372 -5.109 0.000 -9.695 -4.318
C(variety)[5] -6.4399 1.357 -4.746 0.000 -9.100 -3.780
C(variety)[6] -5.6835 1.344 -4.230 0.000 -8.317 -3.050
C(variety)[7] -5.4841 1.341 -4.090 0.000 -8.112 -2.856
C(variety)[8] -4.7126 1.331 -3.539 0.000 -7.322 -2.103
C(variety)[9] -4.5546 1.330 -3.425 0.001 -7.161 -1.948
C(variety)[10] -3.8016 1.320 -2.881 0.004 -6.388 -1.215
C(site)[T.2] 1.6391 1.443 1.136 0.256 -1.190 4.468
C(site)[T.3] 3.3265 1.349 2.466 0.014 0.682 5.971
C(site)[T.4] 3.5822 1.344 2.664 0.008 0.947 6.217
C(site)[T.5] 3.5831 1.344 2.665 0.008 0.948 6.218
C(site)[T.6] 3.8933 1.340 2.905 0.004 1.266 6.520
C(site)[T.7] 4.7300 1.335 3.544 0.000 2.114 7.346
C(site)[T.8] 5.5227 1.335 4.138 0.000 2.907 8.139
C(site)[T.9] 6.7946 1.341 5.068 0.000 4.167 9.422
==================================================================================
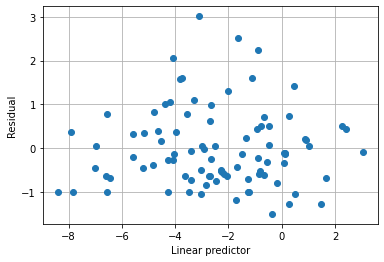
The plot below shows that the default variance function is not capturing the variance structure very well. Also note that the scale parameter estimate is quite small.
[5]:
plt.clf()
plt.grid(True)
plt.plot(result1.predict(linear=True), result1.resid_pearson, 'o')
plt.xlabel("Linear predictor")
plt.ylabel("Residual")
[5]:
Text(0, 0.5, 'Residual')
An alternative variance function is mu^2 * (1 - mu)^2.
[6]:
class vf(sm.families.varfuncs.VarianceFunction):
def __call__(self, mu):
return mu**2 * (1 - mu)**2
def deriv(self, mu):
return 2*mu - 6*mu**2 + 4*mu**3
Fit the quasi-binomial regression with the alternative variance function.
[7]:
bin = sm.families.Binomial()
bin.variance = vf()
model2 = sm.GLM.from_formula("blotch ~ 0 + C(variety) + C(site)", family=bin, data=df)
result2 = model2.fit(scale="X2")
print(result2.summary())
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: blotch No. Observations: 90
Model: GLM Df Residuals: 72
Model Family: Binomial Df Model: 17
Link Function: logit Scale: 0.98855
Method: IRLS Log-Likelihood: -21.335
Date: Tue, 02 Feb 2021 Deviance: 7.2134
Time: 06:54:51 Pearson chi2: 71.2
No. Iterations: 25
Covariance Type: nonrobust
==================================================================================
coef std err z P>|z| [0.025 0.975]
----------------------------------------------------------------------------------
C(variety)[1] -7.9224 0.445 -17.817 0.000 -8.794 -7.051
C(variety)[2] -8.3897 0.445 -18.868 0.000 -9.261 -7.518
C(variety)[3] -7.8436 0.445 -17.640 0.000 -8.715 -6.972
C(variety)[4] -6.9683 0.445 -15.672 0.000 -7.840 -6.097
C(variety)[5] -6.5697 0.445 -14.775 0.000 -7.441 -5.698
C(variety)[6] -6.5938 0.445 -14.829 0.000 -7.465 -5.722
C(variety)[7] -5.5823 0.445 -12.555 0.000 -6.454 -4.711
C(variety)[8] -4.6598 0.445 -10.480 0.000 -5.531 -3.788
C(variety)[9] -4.7869 0.445 -10.766 0.000 -5.658 -3.915
C(variety)[10] -4.0351 0.445 -9.075 0.000 -4.907 -3.164
C(site)[T.2] 1.3831 0.445 3.111 0.002 0.512 2.255
C(site)[T.3] 3.8601 0.445 8.681 0.000 2.989 4.732
C(site)[T.4] 3.5570 0.445 8.000 0.000 2.686 4.428
C(site)[T.5] 4.1079 0.445 9.239 0.000 3.236 4.979
C(site)[T.6] 4.3054 0.445 9.683 0.000 3.434 5.177
C(site)[T.7] 4.9181 0.445 11.061 0.000 4.047 5.790
C(site)[T.8] 5.6949 0.445 12.808 0.000 4.823 6.566
C(site)[T.9] 7.0676 0.445 15.895 0.000 6.196 7.939
==================================================================================
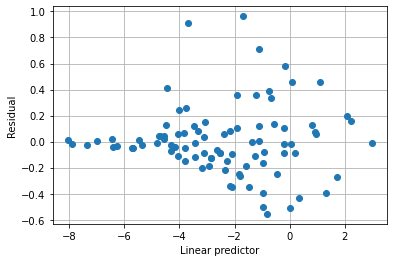
With the alternative variance function, the mean/variance relationship seems to capture the data well, and the estimated scale parameter is close to 1.
[8]:
plt.clf()
plt.grid(True)
plt.plot(result2.predict(linear=True), result2.resid_pearson, 'o')
plt.xlabel("Linear predictor")
plt.ylabel("Residual")
[8]:
Text(0, 0.5, 'Residual')