Linear Mixed Effects Models¶
[1]:
%matplotlib inline
import numpy as np
import pandas as pd
import statsmodels.api as sm
import statsmodels.formula.api as smf
from statsmodels.tools.sm_exceptions import ConvergenceWarning
Note: The R code and the results in this notebook has been converted to markdown so that R is not required to build the documents. The R results in the notebook were computed using R 3.5.1 and lme4 1.1.
%load_ext rpy2.ipython
%R library(lme4)
array(['lme4', 'Matrix', 'tools', 'stats', 'graphics', 'grDevices',
'utils', 'datasets', 'methods', 'base'], dtype='<U9')
Comparing R lmer to statsmodels MixedLM¶
The statsmodels imputation of linear mixed models (MixedLM) closely follows the approach outlined in Lindstrom and Bates (JASA 1988). This is also the approach followed in the R package LME4. Other packages such as Stata, SAS, etc. should also be consistent with this approach, as the basic techniques in this area are mostly mature.
Here we show how linear mixed models can be fit using the MixedLM procedure in statsmodels. Results from R (LME4) are included for comparison.
Here are our import statements:
Growth curves of pigs¶
These are longitudinal data from a factorial experiment. The outcome variable is the weight of each pig, and the only predictor variable we will use here is “time”. First we fit a model that expresses the mean weight as a linear function of time, with a random intercept for each pig. The model is specified using formulas. Since the random effects structure is not specified, the default random effects structure (a random intercept for each group) is automatically used.
[2]:
data = sm.datasets.get_rdataset("dietox", "geepack").data
md = smf.mixedlm("Weight ~ Time", data, groups=data["Pig"])
mdf = md.fit(method=["lbfgs"])
print(mdf.summary())
Mixed Linear Model Regression Results
========================================================
Model: MixedLM Dependent Variable: Weight
No. Observations: 861 Method: REML
No. Groups: 72 Scale: 11.3669
Min. group size: 11 Log-Likelihood: -2404.7753
Max. group size: 12 Converged: Yes
Mean group size: 12.0
--------------------------------------------------------
Coef. Std.Err. z P>|z| [0.025 0.975]
--------------------------------------------------------
Intercept 15.724 0.788 19.952 0.000 14.179 17.268
Time 6.943 0.033 207.939 0.000 6.877 7.008
Group Var 40.395 2.149
========================================================
Here is the same model fit in R using LMER:
%%R
data(dietox, package='geepack')
%R print(summary(lmer('Weight ~ Time + (1|Pig)', data=dietox)))
Linear mixed model fit by REML ['lmerMod']
Formula: Weight ~ Time + (1 | Pig)
Data: dietox
REML criterion at convergence: 4809.6
Scaled residuals:
Min 1Q Median 3Q Max
-4.7118 -0.5696 -0.0943 0.4877 4.7732
Random effects:
Groups Name Variance Std.Dev.
Pig (Intercept) 40.39 6.356
Residual 11.37 3.371
Number of obs: 861, groups: Pig, 72
Fixed effects:
Estimate Std. Error t value
(Intercept) 15.72352 0.78805 19.95
Time 6.94251 0.03339 207.94
Correlation of Fixed Effects:
(Intr)
Time -0.275
Note that in the statsmodels summary of results, the fixed effects and random effects parameter estimates are shown in a single table. The random effect for animal is labeled “Intercept RE” in the statsmodels output above. In the LME4 output, this effect is the pig intercept under the random effects section.
There has been a lot of debate about whether the standard errors for random effect variance and covariance parameters are useful. In LME4, these standard errors are not displayed, because the authors of the package believe they are not very informative. While there is good reason to question their utility, we elected to include the standard errors in the summary table, but do not show the corresponding Wald confidence intervals.
Next we fit a model with two random effects for each animal: a random intercept, and a random slope (with respect to time). This means that each pig may have a different baseline weight, as well as growing at a different rate. The formula specifies that “Time” is a covariate with a random coefficient. By default, formulas always include an intercept (which could be suppressed here using “0 + Time” as the formula).
[3]:
md = smf.mixedlm("Weight ~ Time", data, groups=data["Pig"], re_formula="~Time")
mdf = md.fit(method=["lbfgs"])
print(mdf.summary())
Mixed Linear Model Regression Results
===========================================================
Model: MixedLM Dependent Variable: Weight
No. Observations: 861 Method: REML
No. Groups: 72 Scale: 6.0372
Min. group size: 11 Log-Likelihood: -2217.0475
Max. group size: 12 Converged: Yes
Mean group size: 12.0
-----------------------------------------------------------
Coef. Std.Err. z P>|z| [0.025 0.975]
-----------------------------------------------------------
Intercept 15.739 0.550 28.603 0.000 14.660 16.817
Time 6.939 0.080 86.925 0.000 6.783 7.095
Group Var 19.503 1.561
Group x Time Cov 0.294 0.153
Time Var 0.416 0.033
===========================================================
Here is the same model fit using LMER in R:
%R print(summary(lmer("Weight ~ Time + (1 + Time | Pig)", data=dietox)))
Linear mixed model fit by REML ['lmerMod']
Formula: Weight ~ Time + (1 + Time | Pig)
Data: dietox
REML criterion at convergence: 4434.1
Scaled residuals:
Min 1Q Median 3Q Max
-6.4286 -0.5529 -0.0416 0.4841 3.5624
Random effects:
Groups Name Variance Std.Dev. Corr
Pig (Intercept) 19.493 4.415
Time 0.416 0.645 0.10
Residual 6.038 2.457
Number of obs: 861, groups: Pig, 72
Fixed effects:
Estimate Std. Error t value
(Intercept) 15.73865 0.55012 28.61
Time 6.93901 0.07982 86.93
Correlation of Fixed Effects:
(Intr)
Time 0.006
The random intercept and random slope are only weakly correlated
[4]:
0.294 / (19.493 * 0.416) ** 0.5
[4]:
0.10324316832591753
[5]:
md = smf.mixedlm("Weight ~ Time", data, groups=data["Pig"], re_formula="~Time")
free = sm.regression.mixed_linear_model.MixedLMParams.from_components(
np.ones(2), np.eye(2)
)
mdf = md.fit(free=free, method=["lbfgs"])
print(mdf.summary())
Mixed Linear Model Regression Results
===========================================================
Model: MixedLM Dependent Variable: Weight
No. Observations: 861 Method: REML
No. Groups: 72 Scale: 6.0283
Min. group size: 11 Log-Likelihood: -2217.3481
Max. group size: 12 Converged: Yes
Mean group size: 12.0
-----------------------------------------------------------
Coef. Std.Err. z P>|z| [0.025 0.975]
-----------------------------------------------------------
Intercept 15.739 0.554 28.388 0.000 14.652 16.825
Time 6.939 0.080 86.248 0.000 6.781 7.097
Group Var 19.837 1.571
Group x Time Cov 0.000 0.000
Time Var 0.423 0.033
===========================================================
The likelihood drops by 0.3 when we fix the correlation parameter to 0. Comparing 2 x 0.3 = 0.6 to the chi^2 1 df reference distribution suggests that the data are very consistent with a model in which this parameter is equal to 0.
Here is the same model fit using LMER in R (note that here R is reporting the REML criterion instead of the likelihood, where the REML criterion is twice the log likelihood):
%R print(summary(lmer("Weight ~ Time + (1 | Pig) + (0 + Time | Pig)", data=dietox)))
Linear mixed model fit by REML ['lmerMod']
Formula: Weight ~ Time + (1 | Pig) + (0 + Time | Pig)
Data: dietox
REML criterion at convergence: 4434.7
Scaled residuals:
Min 1Q Median 3Q Max
-6.4281 -0.5527 -0.0405 0.4840 3.5661
Random effects:
Groups Name Variance Std.Dev.
Pig (Intercept) 19.8404 4.4543
Pig.1 Time 0.4234 0.6507
Residual 6.0282 2.4552
Number of obs: 861, groups: Pig, 72
Fixed effects:
Estimate Std. Error t value
(Intercept) 15.73875 0.55444 28.39
Time 6.93899 0.08045 86.25
Correlation of Fixed Effects:
(Intr)
Time -0.086
Sitka growth data¶
This is one of the example data sets provided in the LMER R library. The outcome variable is the size of the tree, and the covariate used here is a time value. The data are grouped by tree.
[6]:
data = sm.datasets.get_rdataset("Sitka", "MASS").data
endog = data["size"]
data["Intercept"] = 1
exog = data[["Intercept", "Time"]]
Here is the statsmodels LME fit for a basic model with a random intercept. We are passing the endog and exog data directly to the LME init function as arrays. Also note that endog_re is specified explicitly in argument 4 as a random intercept (although this would also be the default if it were not specified).
[7]:
md = sm.MixedLM(endog, exog, groups=data["tree"], exog_re=exog["Intercept"])
mdf = md.fit()
print(mdf.summary())
Mixed Linear Model Regression Results
=======================================================
Model: MixedLM Dependent Variable: size
No. Observations: 395 Method: REML
No. Groups: 79 Scale: 0.0392
Min. group size: 5 Log-Likelihood: -82.3884
Max. group size: 5 Converged: Yes
Mean group size: 5.0
-------------------------------------------------------
Coef. Std.Err. z P>|z| [0.025 0.975]
-------------------------------------------------------
Intercept 2.273 0.088 25.864 0.000 2.101 2.446
Time 0.013 0.000 47.796 0.000 0.012 0.013
Intercept Var 0.374 0.345
=======================================================
Here is the same model fit in R using LMER:
%R
data(Sitka, package="MASS")
print(summary(lmer("size ~ Time + (1 | tree)", data=Sitka)))
Linear mixed model fit by REML ['lmerMod']
Formula: size ~ Time + (1 | tree)
Data: Sitka
REML criterion at convergence: 164.8
Scaled residuals:
Min 1Q Median 3Q Max
-2.9979 -0.5169 0.1576 0.5392 4.4012
Random effects:
Groups Name Variance Std.Dev.
tree (Intercept) 0.37451 0.612
Residual 0.03921 0.198
Number of obs: 395, groups: tree, 79
Fixed effects:
Estimate Std. Error t value
(Intercept) 2.2732443 0.0878955 25.86
Time 0.0126855 0.0002654 47.80
Correlation of Fixed Effects:
(Intr)
Time -0.611
We can now try to add a random slope. We start with R this time. From the code and output below we see that the REML estimate of the variance of the random slope is nearly zero.
%R print(summary(lmer("size ~ Time + (1 + Time | tree)", data=Sitka)))
Linear mixed model fit by REML ['lmerMod']
Formula: size ~ Time + (1 + Time | tree)
Data: Sitka
REML criterion at convergence: 153.4
Scaled residuals:
Min 1Q Median 3Q Max
-2.7609 -0.5173 0.1188 0.5270 3.5466
Random effects:
Groups Name Variance Std.Dev. Corr
tree (Intercept) 2.217e-01 0.470842
Time 3.288e-06 0.001813 -0.17
Residual 3.634e-02 0.190642
Number of obs: 395, groups: tree, 79
Fixed effects:
Estimate Std. Error t value
(Intercept) 2.273244 0.074655 30.45
Time 0.012686 0.000327 38.80
Correlation of Fixed Effects:
(Intr)
Time -0.615
convergence code: 0
Model failed to converge with max|grad| = 0.793203 (tol = 0.002, component 1)
Model is nearly unidentifiable: very large eigenvalue
- Rescale variables?
If we run this in statsmodels LME with defaults, we see that the variance estimate is indeed very small, which leads to a warning about the solution being on the boundary of the parameter space. The regression slopes agree very well with R, but the likelihood value is much higher than that returned by R.
[8]:
exog_re = exog.copy()
md = sm.MixedLM(endog, exog, data["tree"], exog_re)
mdf = md.fit()
print(mdf.summary())
Mixed Linear Model Regression Results
===============================================================
Model: MixedLM Dependent Variable: size
No. Observations: 395 Method: REML
No. Groups: 79 Scale: 0.0264
Min. group size: 5 Log-Likelihood: -62.4834
Max. group size: 5 Converged: Yes
Mean group size: 5.0
---------------------------------------------------------------
Coef. Std.Err. z P>|z| [0.025 0.975]
---------------------------------------------------------------
Intercept 2.273 0.101 22.513 0.000 2.075 2.471
Time 0.013 0.000 33.888 0.000 0.012 0.013
Intercept Var 0.646 0.914
Intercept x Time Cov -0.001 0.003
Time Var 0.000 0.000
===============================================================
/opt/hostedtoolcache/Python/3.10.8/x64/lib/python3.10/site-packages/statsmodels/regression/mixed_linear_model.py:2237: ConvergenceWarning: The MLE may be on the boundary of the parameter space.
warnings.warn(msg, ConvergenceWarning)
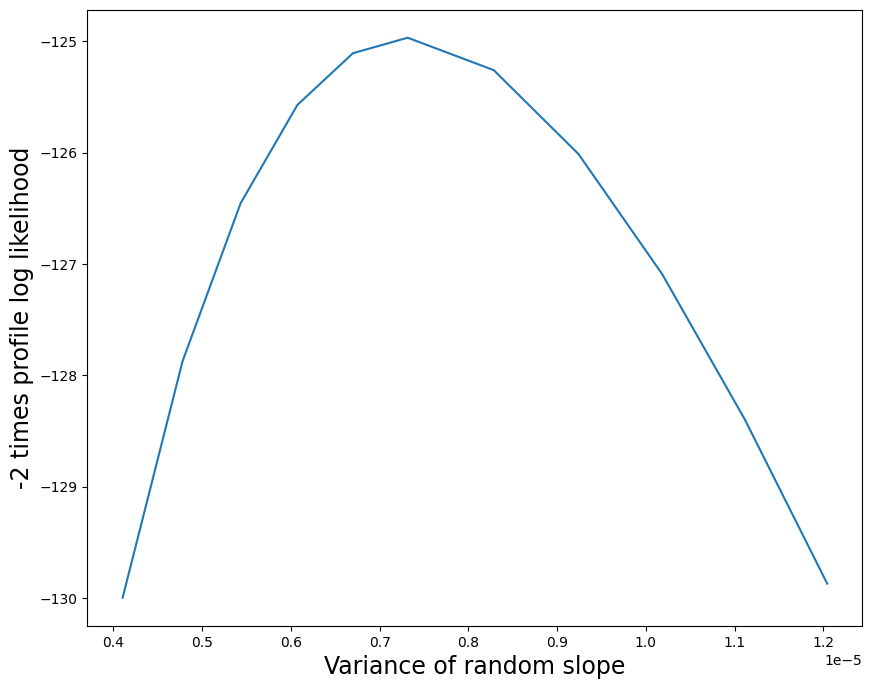
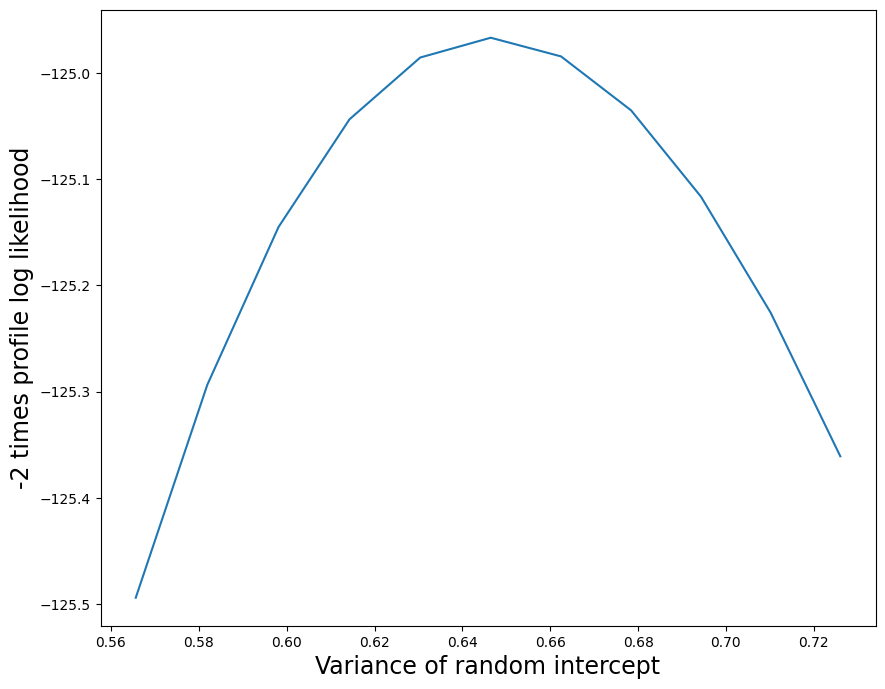
We can further explore the random effects structure by constructing plots of the profile likelihoods. We start with the random intercept, generating a plot of the profile likelihood from 0.1 units below to 0.1 units above the MLE. Since each optimization inside the profile likelihood generates a warning (due to the random slope variance being close to zero), we turn off the warnings here.
[9]:
import warnings
with warnings.catch_warnings():
warnings.filterwarnings("ignore")
likev = mdf.profile_re(0, "re", dist_low=0.1, dist_high=0.1)
Here is a plot of the profile likelihood function. We multiply the log-likelihood difference by 2 to obtain the usual
[10]:
import matplotlib.pyplot as plt
[11]:
plt.figure(figsize=(10, 8))
plt.plot(likev[:, 0], 2 * likev[:, 1])
plt.xlabel("Variance of random intercept", size=17)
plt.ylabel("-2 times profile log likelihood", size=17)
[11]:
Text(0, 0.5, '-2 times profile log likelihood')
Here is a plot of the profile likelihood function. The profile likelihood plot shows that the MLE of the random slope variance parameter is a very small positive number, and that there is low uncertainty in this estimate.
[12]:
re = mdf.cov_re.iloc[1, 1]
with warnings.catch_warnings():
# Parameter is often on the boundary
warnings.simplefilter("ignore", ConvergenceWarning)
likev = mdf.profile_re(1, "re", dist_low=0.5 * re, dist_high=0.8 * re)
plt.figure(figsize=(10, 8))
plt.plot(likev[:, 0], 2 * likev[:, 1])
plt.xlabel("Variance of random slope", size=17)
lbl = plt.ylabel("-2 times profile log likelihood", size=17)