Rolling Regression

Rolling OLS applies OLS across a fixed windows of observations and then rolls (moves or slides) the window across the data set. They key parameter is window which determines the number of observations used in each OLS regression. By default, RollingOLS drops missing values in the window and so will estimate the model using the available data points.

Estimated values are aligned so that models estimated using data points \(i+1, i+2, ... i+window\) are stored in location \(i+window\).

Start by importing the modules that are used in this notebook.

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pandas_datareader as pdr
import seaborn

import statsmodels.api as sm
from statsmodels.regression.rolling import RollingOLS

seaborn.set_style("darkgrid")
pd.plotting.register_matplotlib_converters()
%matplotlib inline

pandas-datareader is used to download data from Ken French’s website. The two data sets downloaded are the 3 Fama-French factors and the 10 industry portfolios. Data is available from 1926.

The data are monthly returns for the factors or industry portfolios.

factors = pdr.get_data_famafrench("F-F_Research_Data_Factors", start="1-1-1926")[0]
factors.head()

	Mkt-RF	SMB	HML	RF
Date
1926-07	2.96	-2.56	-2.43	0.22
1926-08	2.64	-1.17	3.82	0.25
1926-09	0.36	-1.40	0.13	0.23
1926-10	-3.24	-0.09	0.70	0.32
1926-11	2.53	-0.10	-0.51	0.31

industries = pdr.get_data_famafrench("10_Industry_Portfolios", start="1-1-1926")[0]
industries.head()

	NoDur	Durbl	Manuf	Enrgy	HiTec	Telcm	Shops	Hlth	Utils	Other
Date
1926-07	1.45	15.55	4.69	-1.18	2.90	0.83	0.11	1.77	7.04	2.13
1926-08	3.97	3.68	2.81	3.47	2.66	2.17	-0.71	4.25	-1.69	4.35
1926-09	1.14	4.80	1.15	-3.39	-0.38	2.41	0.21	0.69	2.04	0.29
1926-10	-1.24	-8.23	-3.63	-0.78	-4.58	-0.11	-2.29	-0.57	-2.63	-2.84
1926-11	5.20	-0.19	4.10	0.01	4.71	1.63	6.43	5.42	3.71	2.11

The first model estimated is a rolling version of the CAPM that regresses the excess return of Technology sector firms on the excess return of the market.

The window is 60 months, and so results are available after the first 60 (window) months. The first 59 (window - 1) estimates are all nan filled.

endog = industries.HiTec - factors.RF.values
exog = sm.add_constant(factors["Mkt-RF"])
rols = RollingOLS(endog, exog, window=60)
rres = rols.fit()
params = rres.params.copy()
params.index = np.arange(1, params.shape[0] + 1)
params.head()

	const	Mkt-RF
1	NaN	NaN
2	NaN	NaN
3	NaN	NaN
4	NaN	NaN
5	NaN	NaN

params.iloc[57:62]

	const	Mkt-RF
58	NaN	NaN
59	NaN	NaN
60	0.876155	1.399240
61	0.879936	1.406578
62	0.953169	1.408826

params.tail()

	const	Mkt-RF
1151	0.423244	1.075711
1152	0.485909	1.073983
1153	0.475580	1.077410
1154	0.401022	1.083659
1155	0.400929	1.097478

We next plot the market loading along with a 95% point-wise confidence interval. The alpha=False omits the constant column, if present.

fig = rres.plot_recursive_coefficient(variables=["Mkt-RF"], figsize=(14, 6))

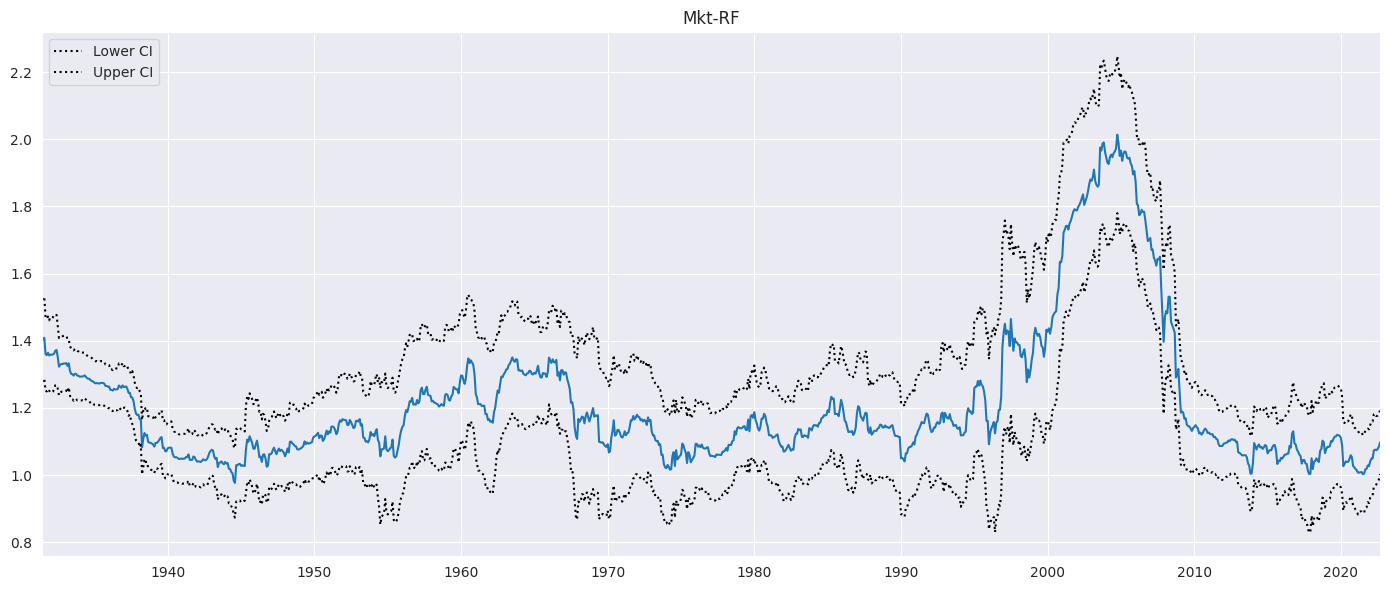
Next, the model is expanded to include all three factors, the excess market, the size factor and the value factor.

exog_vars = ["Mkt-RF", "SMB", "HML"]
exog = sm.add_constant(factors[exog_vars])
rols = RollingOLS(endog, exog, window=60)
rres = rols.fit()
fig = rres.plot_recursive_coefficient(variables=exog_vars, figsize=(14, 18))

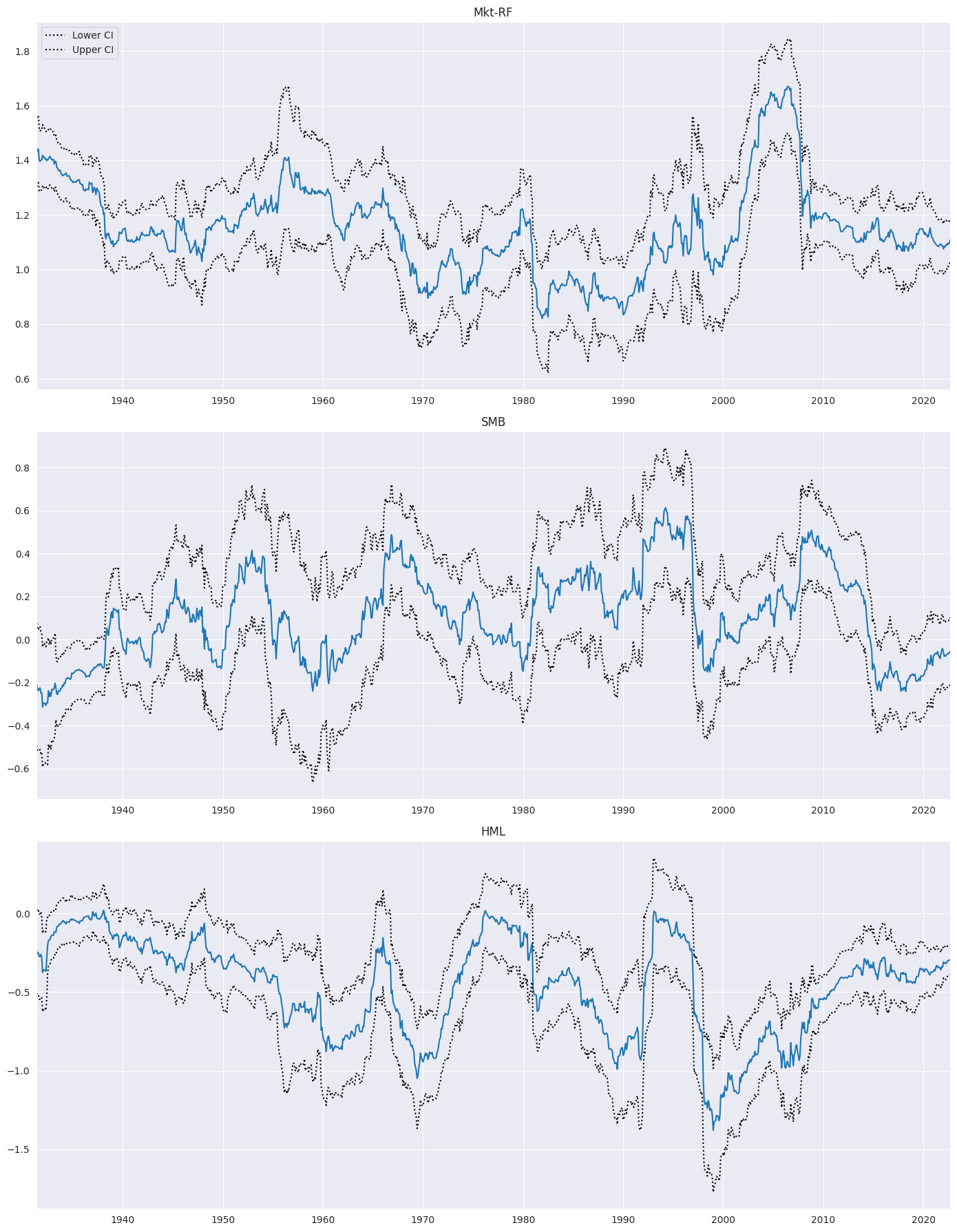
Formulas

RollingOLS and RollingWLS both support model specification using the formula interface. The example below is equivalent to the 3-factor model estimated previously. Note that one variable is renamed to have a valid Python variable name.

joined = pd.concat([factors, industries], axis=1)
joined["Mkt_RF"] = joined["Mkt-RF"]
mod = RollingOLS.from_formula("HiTec ~ Mkt_RF + SMB + HML", data=joined, window=60)
rres = mod.fit()
rres.params.tail()

	Intercept	Mkt_RF	SMB	HML
Date
2022-05	0.483232	1.087113	-0.073053	-0.317213
2022-06	0.502051	1.094325	-0.069356	-0.305908
2022-07	0.481749	1.091095	-0.066826	-0.304270
2022-08	0.427122	1.095873	-0.067418	-0.302008
2022-09	0.414534	1.105376	-0.056993	-0.298265

RollingWLS: Rolling Weighted Least Squares

The rolling module also provides RollingWLS which takes an optional weights input to perform rolling weighted least squares. It produces results that match WLS when applied to rolling windows of data.

Fit Options

Fit accepts other optional keywords to set the covariance estimator. Only two estimators are supported, 'nonrobust' (the classic OLS estimator) and 'HC0' which is White’s heteroskedasticity robust estimator.

You can set params_only=True to only estimate the model parameters. This is substantially faster than computing the full set of values required to perform inference.

Finally, the parameter reset can be set to a positive integer to control estimation error in very long samples. RollingOLS avoids the full matrix product when rolling by only adding the most recent observation and removing the dropped observation as it rolls through the sample. Setting reset uses the full inner product every reset periods. In most applications this parameter can be omitted.

%timeit rols.fit()
%timeit rols.fit(params_only=True)

255 ms ± 2.81 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
62.2 ms ± 686 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

Expanding Sample

It is possible to expand the sample until sufficient observations are available for the full window length. In this example, we start once we have 12 observations available, and then increase the sample until we have 60 observations available. The first non-nan value is computed using 12 observations, the second 13, and so on. All other estimates are computed using 60 observations.

res = RollingOLS(endog, exog, window=60, min_nobs=12, expanding=True).fit()
res.params.iloc[10:15]

	const	Mkt-RF	SMB	HML
Date
1927-05	NaN	NaN	NaN	NaN
1927-06	1.560283	0.999383	1.351219	-0.471879
1927-07	1.235899	1.294857	0.742924	-0.540048
1927-08	1.249999	1.297546	0.752327	-0.548306
1927-09	1.375626	1.286724	1.177758	-0.609331

res.nobs[10:15]

Date
1927-05     0
1927-06    12
1927-07    13
1927-08    14
1927-09    15
Freq: M, dtype: int64